Proving Memoization Correctness in Lean: A Case Study

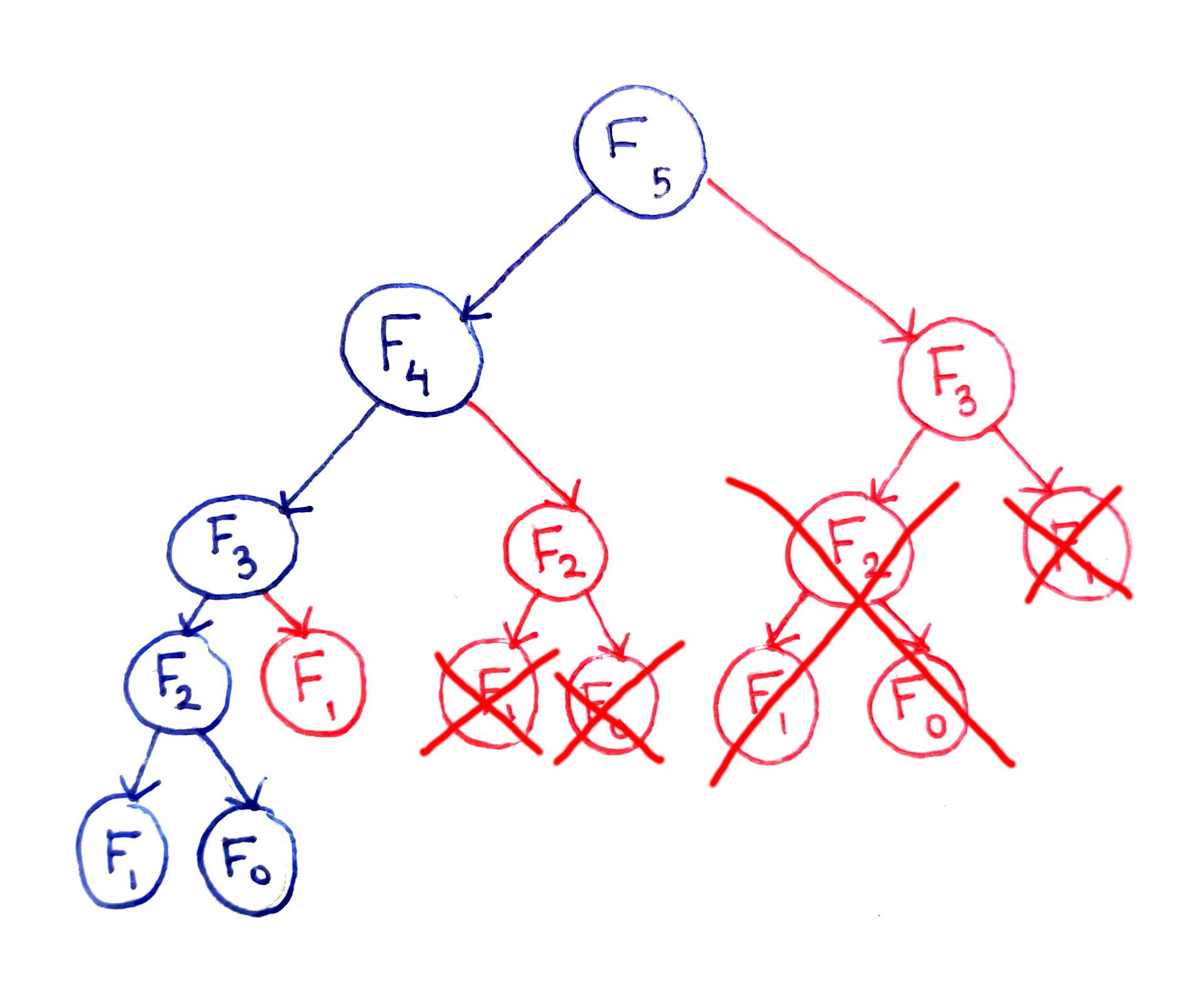
This blog post demonstrates how to solve a dynamic programming problem using memoization in the Lean theorem prover and formally verify its correctness. The author tackles the Bytelandian Gold Coins problem, initially presenting a memoized solution using a HashMap. The difficulty of directly proving its correctness is highlighted due to challenges in reasoning about data structure invariants. The solution leverages subtypes and dependent pairs to create a `PropMap`, a memoization table that stores not only computed values but also proofs of their correctness. The algorithm's correctness is then proven incrementally within the recursive implementation itself, culminating in a trivial top-level proof. This approach elegantly intertwines code and proof, showcasing a powerful technique for formally verifying dynamic programming algorithms.