Webtagr - Technology News Summarizer

Nonlinear Generalization of Maxwell's Equations from a Variational Approach

2025-04-20

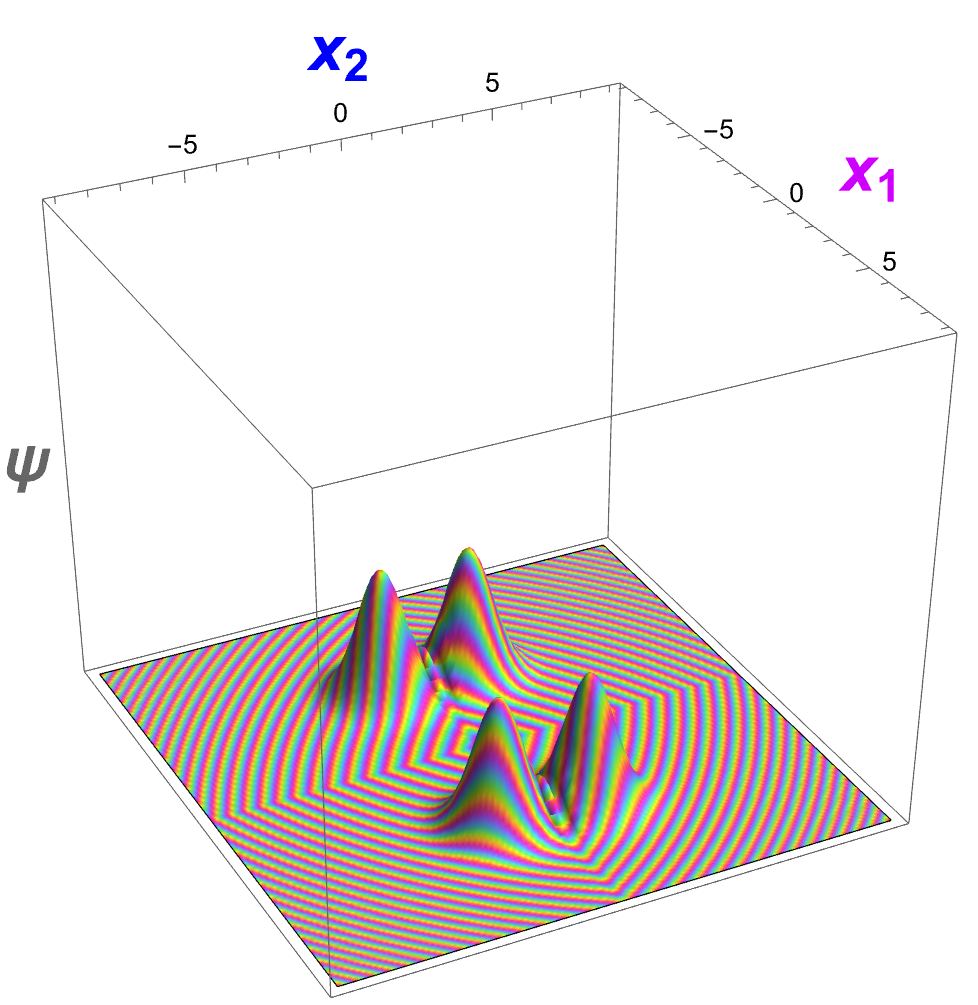
This research article derives a nonlinear generalization of Maxwell's equations from a variational approach where the action measures the variability of the metric tensor. The space is a Weyl space where the metric tensor's covariant derivative needn't vanish. The Lorentz force law is derived as a geodesic equation. Charge density obeys a covariant wave equation, suggesting it's a field propagating at light speed, supporting the wave nature of electrons. The Dirac equation is also shown to be geometric. The link between the Lorentz force and spacetime's metric directly explains Zitterbewegung and quantum mechanical waves.

(iopscience.iop.org)

Physics Maxwell's Equations Nonlinear Generalization

Challenge to Quantum Theory: Could 'Paraparticles' Exist in 3D?

2025-04-12

For decades, physicists have believed that only two fundamental particles exist: bosons and fermions. This belief is largely based on the DHR theorem and its underlying assumptions. However, new research suggests the possibility of a third type of particle, called a 'paraparticle,' in three dimensions. These particles possess hidden internal states that change when particles swap places, but these changes disappear during measurement. This discovery challenges conventional quantum theory and opens new avenues for research in quantum computing and condensed matter physics.

(www.quantamagazine.org)

Physics quantum theory paraparticles DHR theorem

Quantum Double-Slit: Did the Particle Go Through Both Slits?

2025-03-16

This post tackles a central question in the quantum double-slit experiment: how do particles create an interference pattern? Using a simplified 'double-door' analogy, the author argues that neither the particle itself nor its wave function passes through both slits simultaneously. A particle can only occupy one position, while the wave function resides in possibility space, not physical space. The interference pattern doesn't arise from the particle or wave function's movement in physical space but is linked to the wave function's evolution in possibility space. The post ends on a cliffhanger, promising to explain the source of the interference effect in a future installment.

(profmattstrassler.com)

Physics double slit experiment wave function

Non-Determinism in Classical Mechanics: Norton's Dome and the Space Invader

2025-02-15

Classical mechanics harbors some famously non-deterministic cases. The article first introduces Norton's Dome, where the derivative of the force is undefined at a specific point, leading to non-unique solutions. A more bizarre example is the 'Space Invader,' experiencing unbounded acceleration in finite time, reaching infinity at t=π/2. Painlevé non-collision singularities are also mentioned, such as a five-body gravitational problem where a particle reaches infinity in finite time. These examples challenge the deterministic assumptions of classical mechanics.

(physics.stackexchange.com)

Physics classical mechanics non-determinism Norton's Dome

Heatproof Magnetism: A Surprising Discovery Defies Expectations

2025-01-19

High temperatures are known to disrupt order and patterns. However, physicists have theoretically demonstrated a type of idealized magnetism that maintains its orderly structure regardless of temperature. This surprising discovery stems from a simple question posed at a lecture, leading to a deeper exploration of quantum field theory. Researchers found that in a system resembling two intertwined magnetic grids, a specific magnetic order persists even at infinitely high temperatures. The freely spinning magnetic vectors stabilize the up-down aligned vectors, maintaining overall magnetic order. This finding could have implications for cosmology and the quest to achieve room-temperature quantum phenomena.

(www.quantamagazine.org)

Physics magnetism high temperature

The Truth About the Short Range of the Weak Nuclear Force: It's Not Quantum Mechanics

2025-01-15

A long-standing misconception attributes the short range of the weak nuclear force to the uncertainty principle and virtual particles in quantum mechanics. This article argues that the short range is actually due to the inherent 'stiffness' of the field itself. This 'stiffness' makes it more energetically costly to change the field's value, thus limiting the force's range. While quantum mechanics explains the mass of the W and Z bosons associated with the weak force, this is unrelated to the force's short range. The author uses analogies and mathematical derivations to clearly explain how 'stiffness' leads to both short-range forces and particle mass, correcting a long-held misunderstanding.

(profmattstrassler.com)

Physics weak nuclear force

A Simple Violation of Determinism in Newtonian Mechanics: The Dome

2025-01-03

This paper presents a counterintuitive example in Newtonian mechanics where determinism fails: a mass resting at the apex of a specially shaped dome spontaneously moves without any external intervention. The author demonstrates, through mathematical solutions and physical reasoning, that this system allows for multiple solutions, some of which depict the mass initiating motion at an arbitrary time, with no Newtonian prediction for when or in what direction. Even simple Newtonian systems can exhibit acausal events, challenging the universality of causality in classical physics.

(sites.pitt.edu)

Physics Newtonian mechanics determinism causality

Physicists Measure Quantum Geometry for the First Time

2024-12-24

MIT physicists have, for the first time, measured the quantum geometry of electrons in solids. Using angle-resolved photoemission spectroscopy (ARPES), they overcame a long-standing challenge of directly measuring the geometry of quantum wave functions. This breakthrough opens new avenues for understanding and manipulating the quantum properties of materials, with potential applications in quantum computing and advanced electronics. The team's success involved international collaborations and innovative experimental design, navigating challenges posed by the COVID-19 pandemic.

(phys.org)

Physics quantum geometry quantum materials

Physics' New Frontier: Beyond Thermodynamics

2024-12-22

This article delves into the significance and limitations of thermodynamics in physics. The author argues that while statistical mechanics provides a microscopic understanding of thermodynamics, it may obscure more general principles. A call is made to focus on macroscopic, empirical observations, such as non-equilibrium thermodynamics and self-organizing systems, suggesting these areas may hold new physical laws and offer solutions to practical problems, echoing the initial development of thermodynamics from steam engine improvements.

(scottlocklin.wordpress.com)

Physics non-equilibrium thermodynamics self-organizing systems

LHC Unveils 23 Exotic Hadrons, Challenging Strong Interaction Theories

2024-12-20

The Large Hadron Collider (LHC) has yielded a surprising discovery: 23 exotic hadrons, including pentaquarks and tetraquarks, whose structures defy explanation by current theories. This discovery, akin to a fascinating detective story, is driving theorists to develop new models, such as hadronic molecule models and compact tetraquark models. Future experiments at the High-Luminosity LHC, Belle II, and BESIII will provide more data, offering further clues to unraveling the mysteries of the strong interaction.

(cerncourier.com)

Physics hadrons Large Hadron Collider strong interaction

Physicists Discover Particle with Mass Only When Moving in One Direction

2024-12-19

Scientists have discovered a peculiar quasiparticle, the semi-Dirac fermion, which only exhibits effective mass when moving in one direction. Predicted in 2008, this phenomenon has now been confirmed in a ZrSiS semi-metal crystal at extremely low temperatures (-269°C). Its energy properties differ drastically in perpendicular directions, akin to a train experiencing resistance when switching tracks, thus gaining mass. This discovery could have profound implications for quantum physics and electronic sensors, but further research is needed to explore its applications.

(www.sciencealert.com)

Physics

Exotic New Superconductors Delight and Confound

2024-12-13

Three new types of superconductors were discovered this year, challenging our understanding of this phenomenon. These two-dimensional materials, like graphene, exhibit unprecedented flexibility, switching between insulating, conducting, and superconducting states with simple adjustments. One even defies expectations by strengthening in a magnetic field. These discoveries deepen the mystery of superconductivity while offering hope for room-temperature superconductors, potentially revolutionizing energy and transportation.

(www.quantamagazine.org)

Physics superconductors 2D materials quantum physics

Bizarre Particle's Mass Depends on Travel Direction

2024-12-12

Scientists have unexpectedly discovered a strange quasiparticle, a semi-Dirac fermion, in a ZrSiS material. This particle exhibits a peculiar behavior: it's massless when moving along a specific direction but gains mass when traveling in other directions. This discovery, stemming from research into the properties of quasiparticles within ZrSiS, relates to Einstein's mass-energy equivalence, E=mc². When moving at light speed in a specific direction, the quasiparticle is massless; changing direction and slowing down causes it to gain mass. The finding could potentially lead to novel applications for ZrSiS, similar to those of graphene.

(newatlas.com)

Physics semi-Dirac fermion quasiparticle mass-energy equivalence

Category: Physics