Généralisation non linéaire des équations de Maxwell à partir d'une approche variationnelle
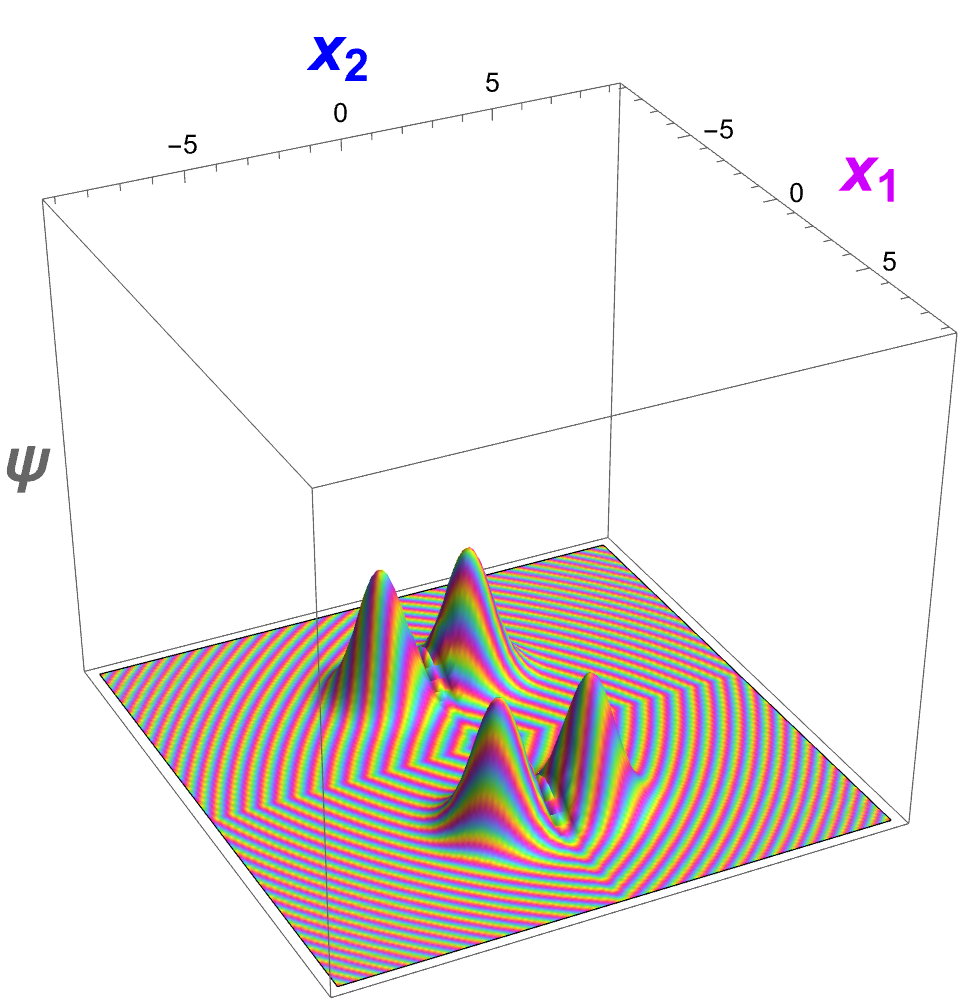
Cet article de recherche dérive une généralisation non linéaire des équations de Maxwell à partir d'une approche variationnelle, où l'action mesure la variabilité du tenseur métrique. L'espace est un espace de Weyl où la dérivée covariante du tenseur métrique n'a pas besoin de s'annuler. La loi de force de Lorentz est dérivée comme une équation géodésique. La densité de charge obéit à une équation d'onde covariante, suggérant qu'il s'agit d'un champ se propageant à la vitesse de la lumière, ce qui soutient la nature ondulatoire des électrons. L'équation de Dirac est également montrée comme étant géométrique. Le lien entre la force de Lorentz et la métrique de l'espace-temps explique directement le Zitterbewegung et les ondes mécaniques quantiques.