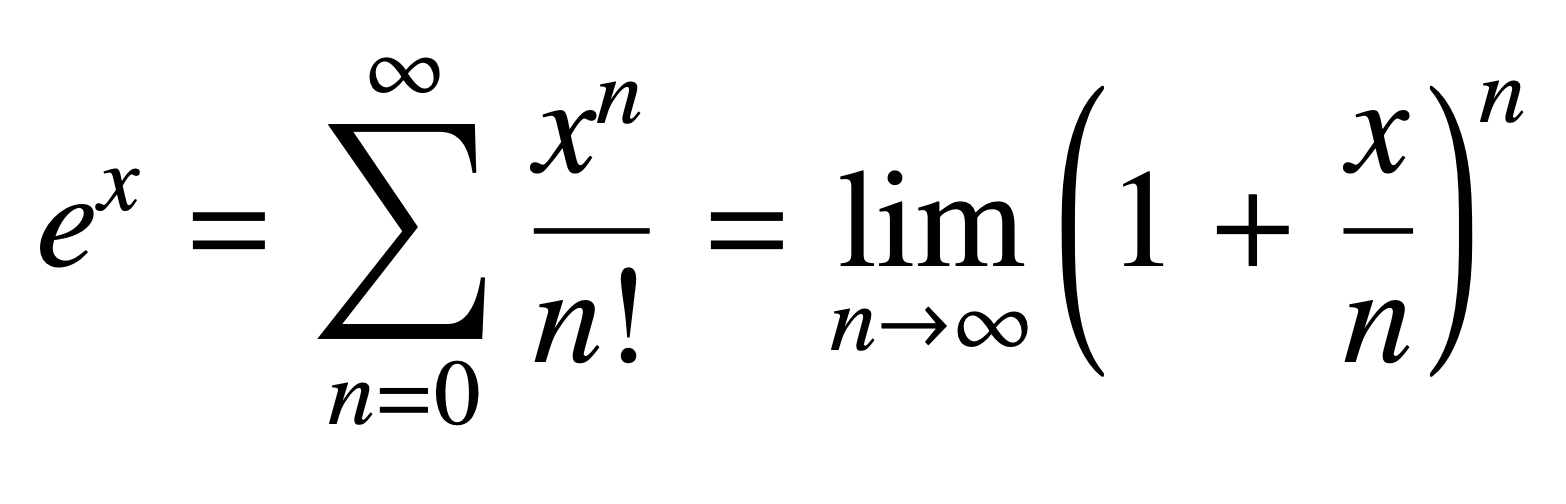Tags populaires：
Virtualisation sécurité DNS vérification formelle analyse d'atteignabilité erreurs du compilateur conflit de macro extension web framework de développement Graphiques bitmap incohérences d'API Tous les tags

Analyse de Fréquence des Symboles Mathématiques : Une Histoire d'Erreurs

2025-06-07
Analyse de Fréquence des Symboles Mathématiques : Une Histoire d'Erreurs

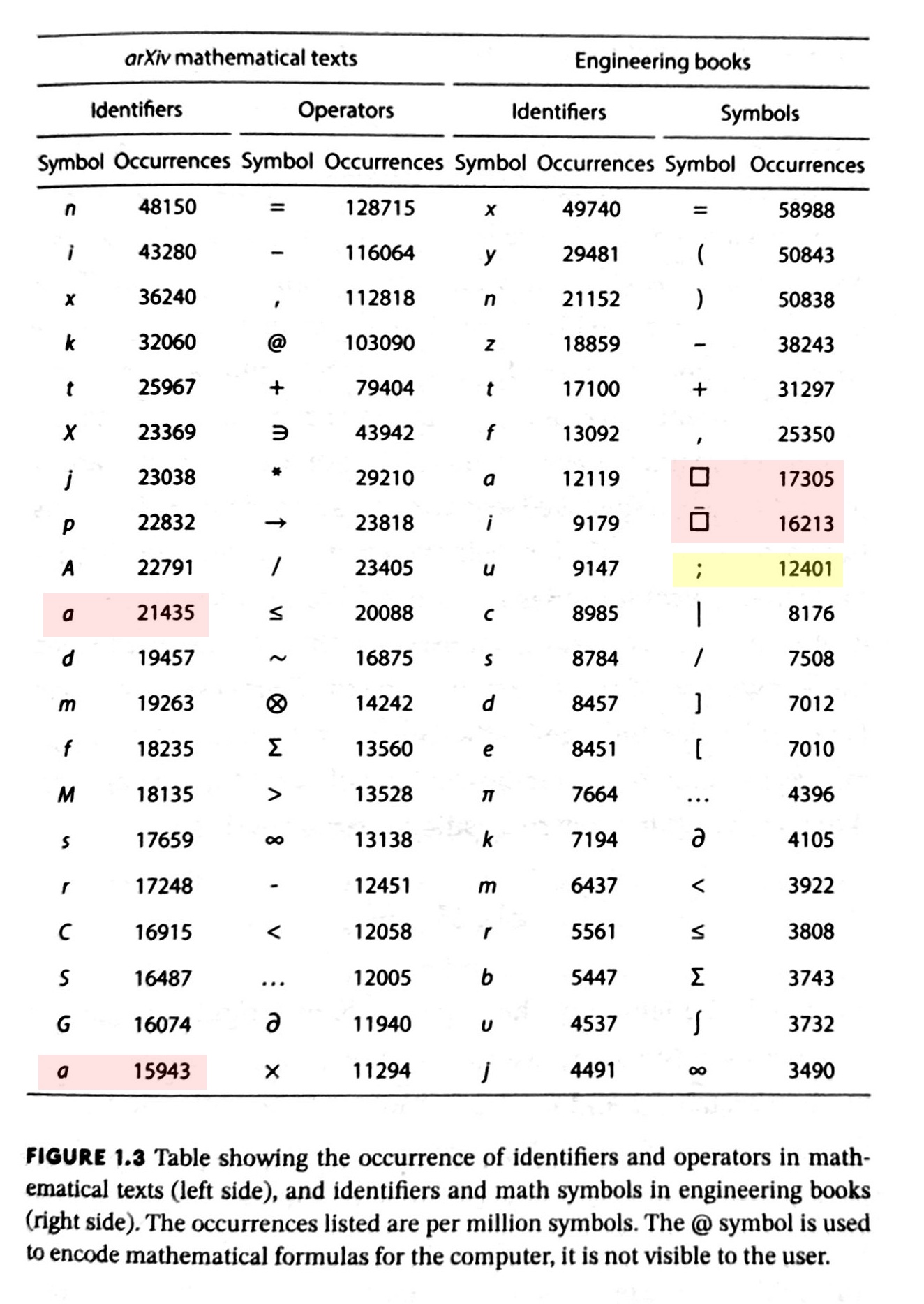
Dr. Drang examine le livre de Raúl Rojas, 'Le Langage des Mathématiques', explorant l'histoire et la standardisation des symboles mathématiques. Un tableau d'analyse de fréquence des symboles, basé sur des articles d'arXiv et des manuels d'ingénierie, a attiré son attention, révélant des erreurs. Des erreurs incluaient un alpha (α) listé comme 'a', et des barres de fraction représentées par deux boîtes. En retraçant l'origine des données, Dr. Drang a découvert que les erreurs provenaient de négligences dans le traitement des données et la composition typographique. L'article souligne non seulement l'histoire des symboles mathématiques, mais aussi l'importance cruciale d'une manipulation rigoureuse des données dans la recherche académique.

Lire plus
(leancrew.com)
Divers symboles mathématiques analyse de fréquence erreurs de données

Pandoc : un convertisseur LaTeX vers MathML étonnamment efficace

2025-05-03
Pandoc : un convertisseur LaTeX vers MathML étonnamment efficace

L'auteur explore plusieurs méthodes pour convertir des équations LaTeX en MathML, et découvre finalement que Pandoc est la plus efficace. Pandoc gère sans effort les équations mono-lignes et multi-lignes, y compris les matrices complexes et les fonctions par morceaux. Bien qu'un petit bogue ait été découvert dans la gestion par Pandoc des équations impliquant des limites et des sommations, ses performances globales sont excellentes. Un script Python est fourni pour nettoyer la sortie MathML de Pandoc et améliorer l'efficacité.

Lire plus
(leancrew.com)
Développement

L'énigme des boulons entrelacés : une solution mathématique à un classique de Gardner

2025-03-07
L'énigme des boulons entrelacés : une solution mathématique à un classique de Gardner

Cet article de blog traite d'une énigme mathématique classique posée par Martin Gardner en 1958 : deux boulons identiques s'engrènent ; si vous les faites tourner comme vos pouces, les têtes des boulons se rapprochent-elles, s'éloignent-elles ou restent-elles à la même distance ? L'auteur fournit une analyse géométrique détaillée expliquant pourquoi les têtes des boulons restent à la même distance, réfutant l'analogie moins intuitive de l'escalator de Gardner. L'article inclut des diagrammes de profils de filetage et des illustrations 3D des boulons de l'auteur pour une meilleure compréhension.

Lire plus
(leancrew.com)
Divers boulons

Dévoiler le mystère du mécanisme d'Anticythère : un code cosmique 254:19

2024-12-15
Dévoiler le mystère du mécanisme d'Anticythère : un code cosmique 254:19

Découvert au Ier siècle av. J.-C., le mécanisme d'Anticythère est un dispositif astronomique complexe capable de suivre les mouvements du soleil, de la lune et des planètes. Son système d'engrenages complexe est étonnant. Cet article explore un rapport d'engrenage spécifique 254:19 au sein du mécanisme, révélant qu'il n'est pas arbitraire, mais un reflet intelligent des mouvements du soleil et de la lune sur un cycle métonique de 19 ans, démontrant la remarquable compréhension de l'astronomie des anciens Grecs. L'article corrige des erreurs antérieures concernant les cycles de Saros et de Méton et explique les principes mathématiques derrière ce rapport d'engrenage, révélant la profonde compréhension des anciens Grecs de la mécanique céleste.

Lire plus
(leancrew.com)
Technologie Mécanisme d'Anticythère Cycle métonique Astronomie