Comprendre la notation Big O : un guide pratique
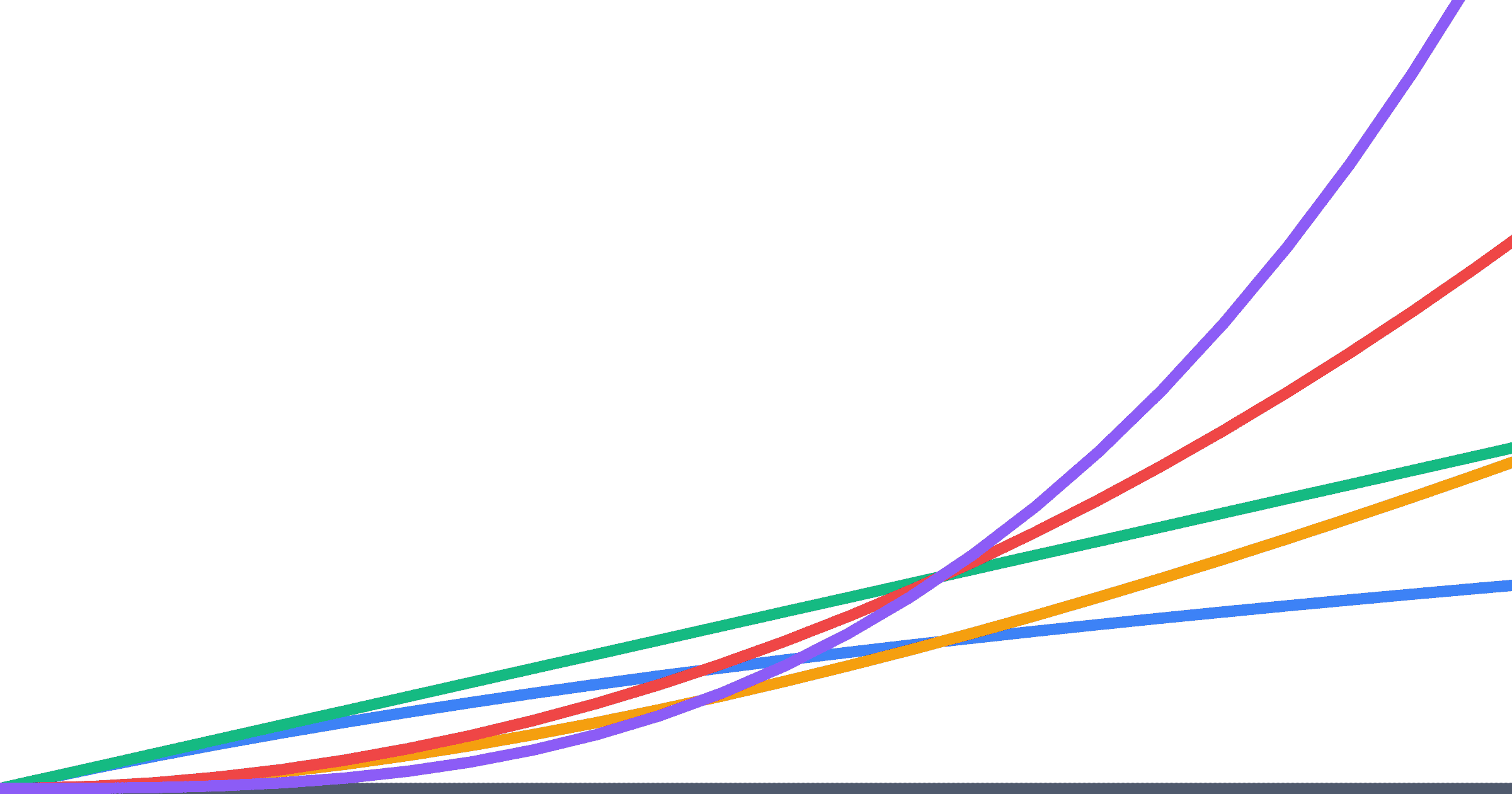
Cet article fournit une explication claire et concise de la notation Big O, une méthode pour décrire les performances des algorithmes. En utilisant la fonction `sum` de JavaScript comme exemple, il compare les différences entre les complexités temporelles O(1) constante, O(log n) logarithmique, O(n) linéaire et O(n²) quadratique. Des visualisations et des exemples de code illustrent les complexités temporelles de plusieurs algorithmes, notamment le tri à bulles et la recherche dichotomique. L'article explore également des techniques pour améliorer les performances du code, telles que l'évitement de `indexOf` dans les boucles et l'utilisation du cache pour réduire les calculs redondants. Enfin, il souligne l'importance des tests empiriques, en mettant en garde contre la confiance aveugle dans les résultats théoriques.
Lire plus