GPT-3's Astonishing Embedding Capacity: High-Dimensional Geometry and the Johnson-Lindenstrauss Lemma
2025-09-15
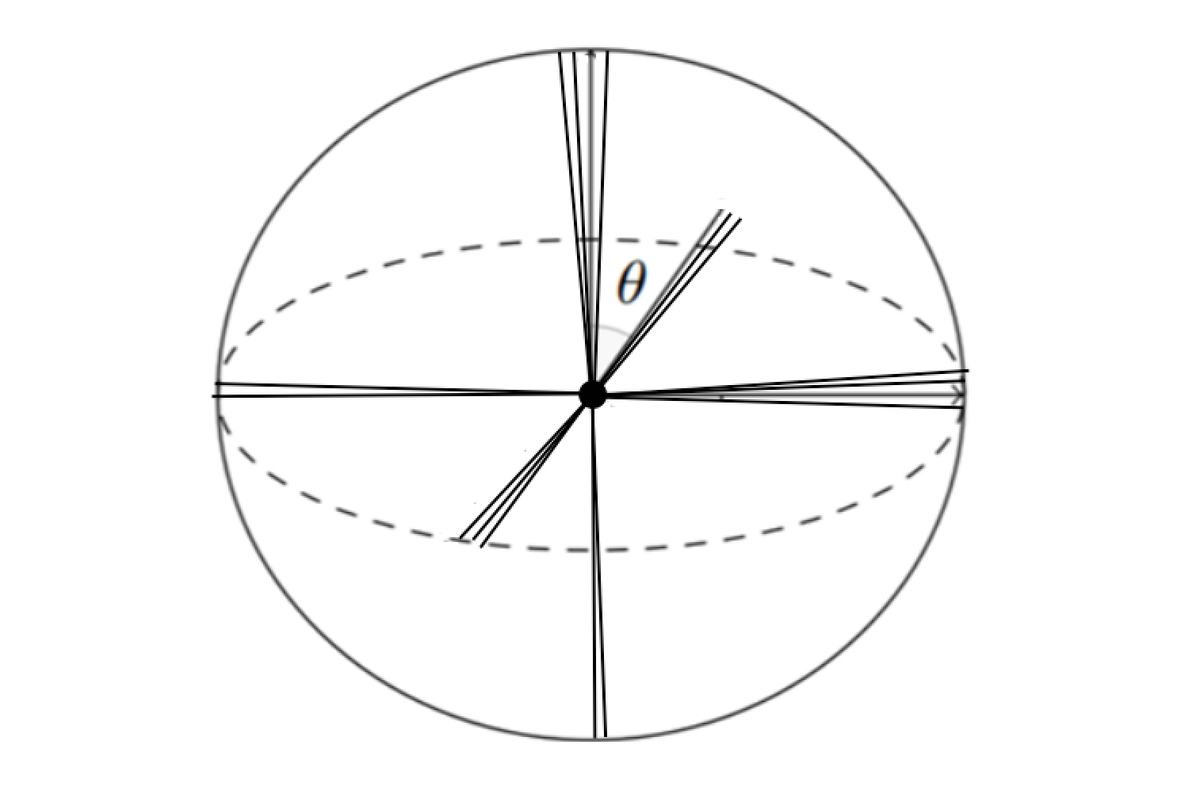
This blog post explores how large language models like GPT-3 accommodate millions of distinct concepts within a relatively modest 12,288-dimensional embedding space. Through experiments and analysis of the Johnson-Lindenstrauss Lemma, the author reveals the importance of 'quasi-orthogonal' vector relationships in high-dimensional geometry and methods for optimizing the arrangement of vectors in embedding spaces to increase capacity. The research finds that even accounting for deviations from perfect orthogonality, GPT-3's embedding space possesses an astonishing capacity sufficient to represent human knowledge and reasoning.