La capacité d'intégration étonnante de GPT-3 : géométrie de haute dimension et lemme de Johnson-Lindenstrauss
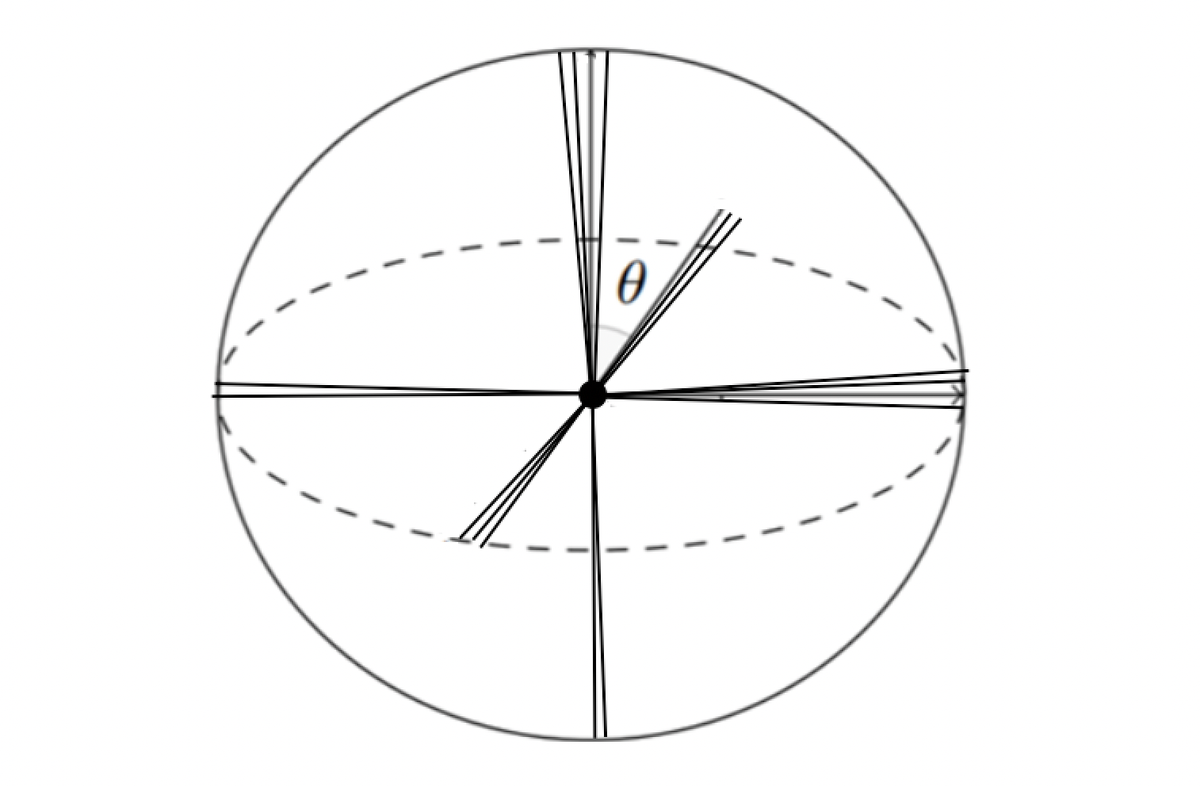
Cet article de blog explore comment les grands modèles de langage comme GPT-3 intègrent des millions de concepts distincts dans un espace d'intégration relativement modeste de 12 288 dimensions. Grâce à des expériences et à l'analyse du lemme de Johnson-Lindenstrauss, l'auteur révèle l'importance des relations vectorielles « quasi-orthogonales » dans la géométrie de haute dimension et les méthodes d'optimisation de la disposition des vecteurs dans les espaces d'intégration pour augmenter la capacité. La recherche montre que, même en tenant compte des écarts par rapport à l'orthogonalité parfaite, l'espace d'intégration de GPT-3 possède une capacité étonnante, suffisante pour représenter les connaissances et le raisonnement humains.