Pi n'est pas constant : exploration de π dans les espaces non euclidiens
2025-09-15
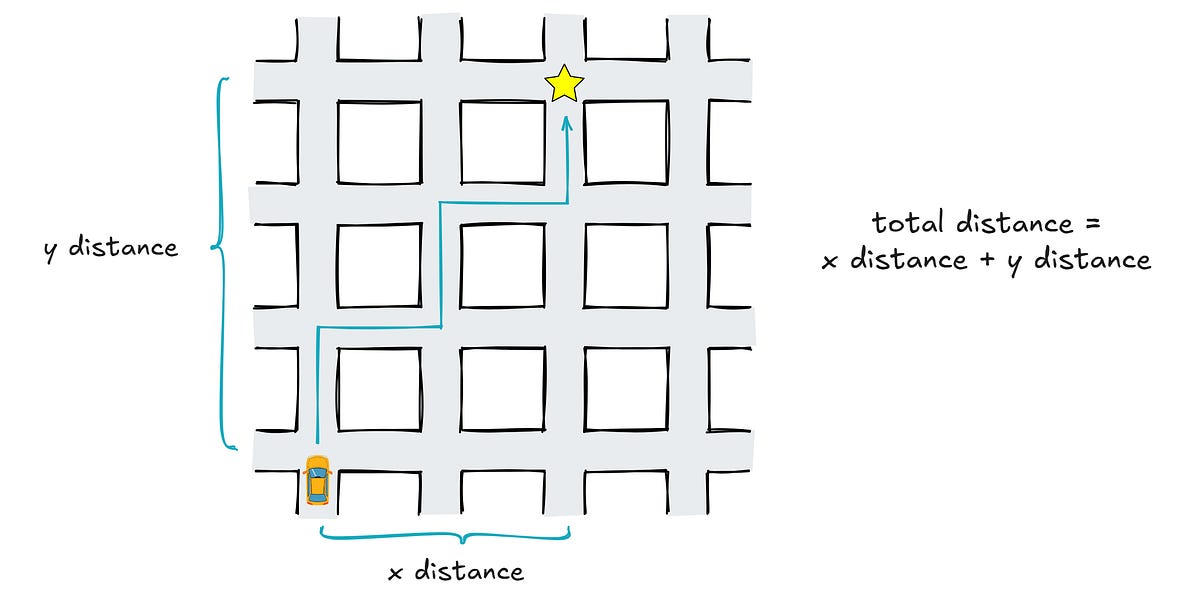
Cet article explore la valeur de pi (π) dans différents espaces métriques. En modifiant la formule de distance en géométrie euclidienne, une série d'espaces non euclidiens sont construits, et le rapport entre la circonférence et le diamètre des « cercles » dans ces espaces est calculé. Les résultats montrent que, tandis que dans l'espace euclidien standard (n=2), π est approximativement égal à 3,14159, sa valeur change dans d'autres espaces. Par exemple, en géométrie du taxi (n=1) et à distance de Chebyshev (n→∞), π est égal à 4. Cela démontre que la valeur de π n'est pas constante, mais dépend de la géométrie sous-jacente de l'espace.
Divers
Géométrie non euclidienne