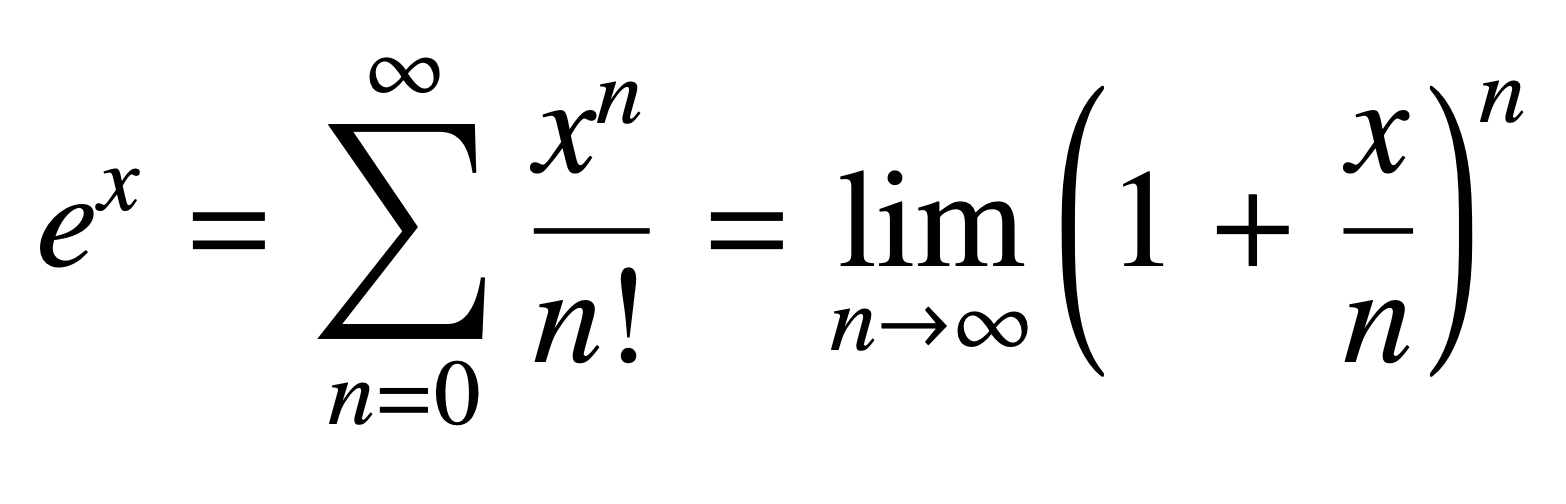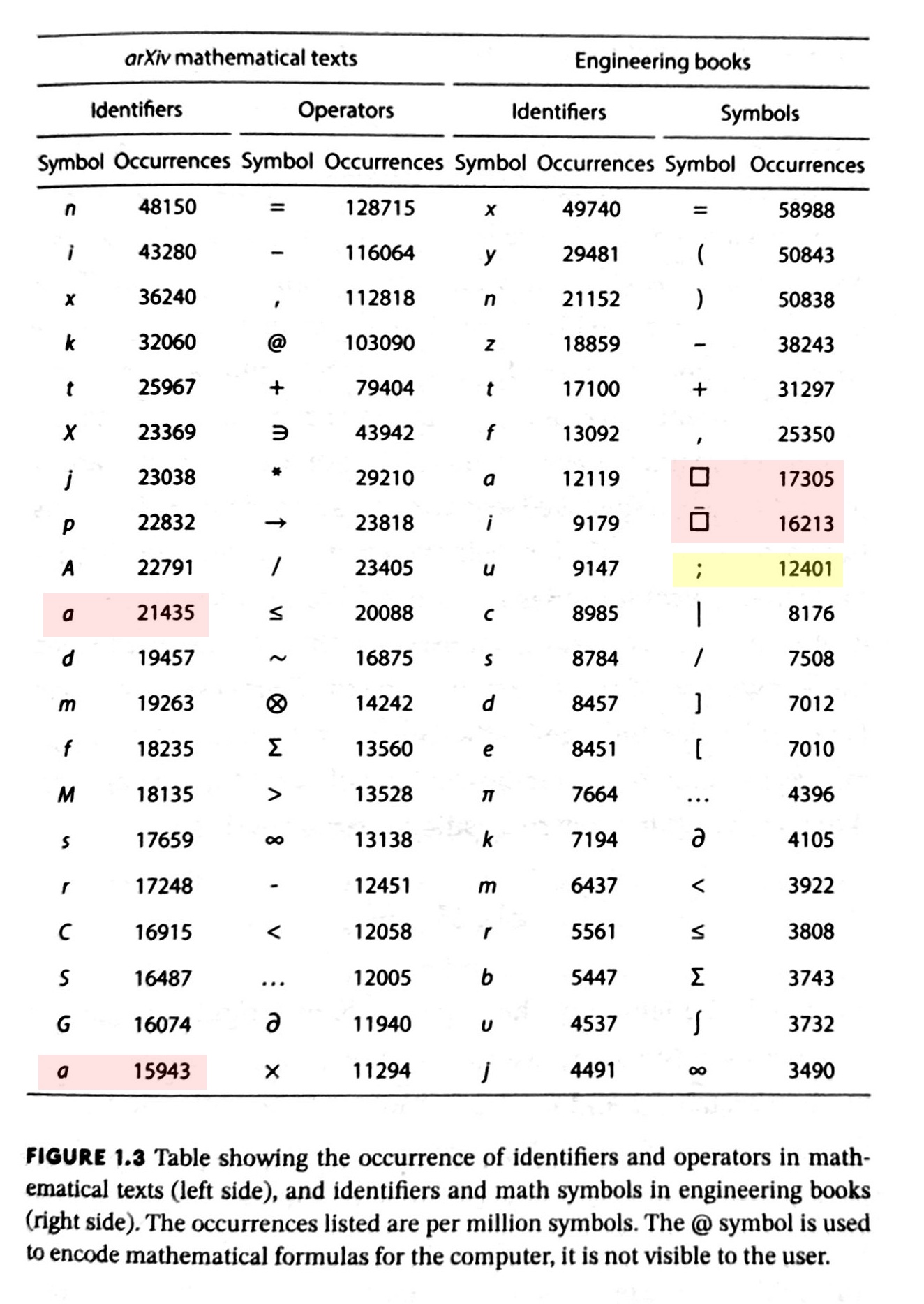
Dr. Drangはラウル・ロハスの著書『数学の言語』をレビューし、数学記号の歴史と標準化を探っています。arXiv論文と工学教科書に基づいた記号の頻度分析表が彼の注意を引きつけ、いくつかの誤りを明らかにしました。アルファ(α)が「a」としてリストされていたり、分数線が2つのボックスとして表現されていたりといった誤りです。データのソースを辿ることで、Dr. Drangはこれらの誤りがデータ処理と組版における不注意によるものであることを突き止めました。この記事は、数学記号の歴史だけでなく、学術研究における厳密なデータ処理の重要性も浮き彫りにしています。
続きを読む
著者はLaTeX式をMathMLに変換する様々な方法を探求し、最終的にPandocが最も効率的であることを発見しました。Pandocは、複雑な行列や区分関数を含む、単一行および複数行の式を簡単に処理します。極限と総和を含む式を処理する際に小さなバグが見つかりましたが、全体的なパフォーマンスは優れており、Pandocの出力をクリーンアップして効率を向上させるPythonスクリプトが提供されています。
続きを読む
この記事では、1958年にマーティン・ガードナーが提示した古典的な数学パズルを取り上げます。2つの同一のボルトが噛み合っています。親指を回すようにボルトを回すと、ボルトの頭は近づきますか、離れますか、それとも同じ距離を保ちますか？著者は、ボルトの頭が同じ距離を保つ理由を説明する詳細な幾何学的分析を行い、ガードナーの直感性に欠けるエスカレーターのアナロジーを反論しています。記事には、ねじ山規格の図と、より良い理解のための著者が作成したボルトの3Dイラストが含まれています。
続きを読む
紀元前1世紀に発見されたアンティキティラ島のメカニズムは、太陽、月、惑星の動きを追跡できる複雑な天文装置です。その精巧な歯車システムは驚くべきものです。この記事では、メカニズム内の特定の歯車比254：19について深く掘り下げ、それが任意のものではなく、19年のメトン周期における太陽と月の動きを巧みに反映したものであることを明らかにし、古代ギリシャ人の天文学への卓越した理解を示しています。この記事では、サロス周期とメトン周期に関するこれまでの誤解を修正し、この歯車比の背後にある数学的原理を説明することで、古代ギリシャ人が天体の動きに対して持っていた深い洞察を明らかにしています。
続きを読む