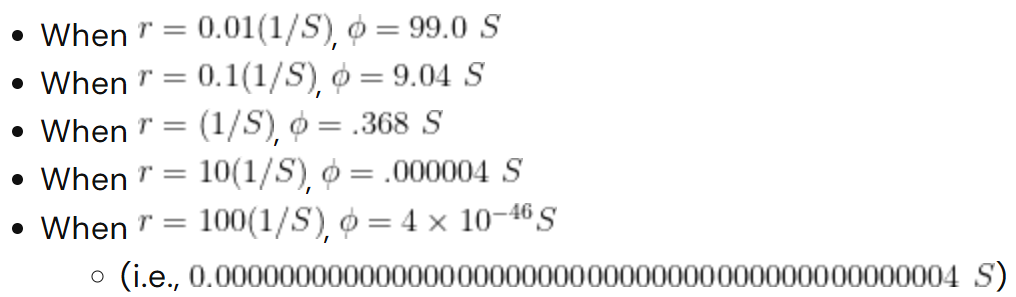Generalização Não Linear das Equações de Maxwell a Partir de uma Abordagem Variacional
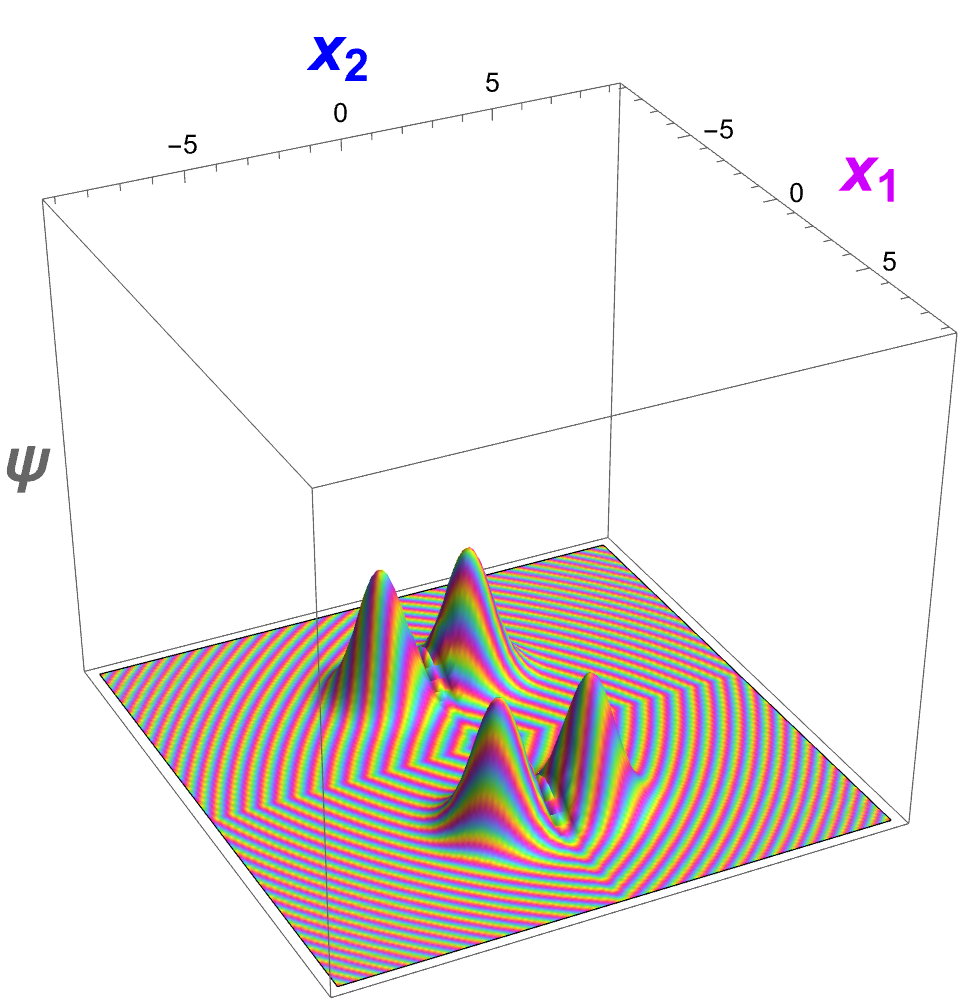
Este artigo de pesquisa deriva uma generalização não linear das equações de Maxwell a partir de uma abordagem variacional, onde a ação mede a variabilidade do tensor métrico. O espaço é um espaço de Weyl, onde a derivada covariante do tensor métrico não precisa ser nula. A lei da força de Lorentz é derivada como uma equação geodésica. A densidade de carga obedece a uma equação de onda covariante, sugerindo que é um campo que se propaga à velocidade da luz, apoiando a natureza ondulatória dos elétrons. A equação de Dirac também é mostrada como geométrica. A ligação entre a força de Lorentz e a métrica do espaço-tempo explica diretamente o Zitterbewegung e as ondas mecânico-quânticas.