Tags populares：
Virtualização segurança DNS verificação formal análise de alcance IA erros do compilador conflito de macro extensão web framework de desenvolvimento Gráficos de Bitmap Todos os tags

O Problema da Aglomeração de Ônibus: Por que Adicionar Ônibus Não Funciona

2025-07-25
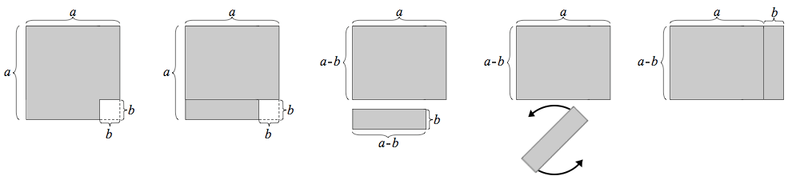
O Problema da Aglomeração de Ônibus: Por que Adicionar Ônibus Não Funciona

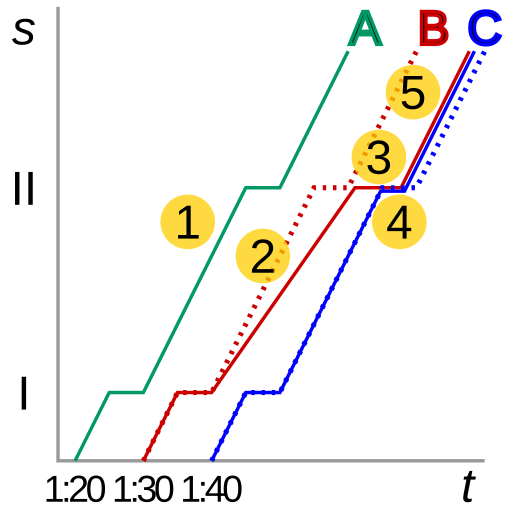
Imagine dois ônibus na mesma rota, funcionando em um horário. Um deles atrasa por causa do trânsito. Este ônibus atrasado pega passageiros que pegariam o ônibus seguinte, causando atrasos ainda maiores. O ônibus seguinte, enquanto isso, faz um tempo melhor devido a menos passageiros. Eventualmente, os ônibus se aglomeram, às vezes com o segundo ônibus ultrapassando o primeiro. Adicionar mais ônibus não é a solução; estratégias melhores incluem gerenciar os tempos de parada, pular paradas, encorajar os passageiros a pegar ônibus posteriores ou, como a Universidade do Norte do Arizona fez, abandonar os horários fixos e controlar manualmente o espaçamento dos ônibus para uma distribuição uniforme.

Leia mais
(www.futilitycloset.com)
Diversos escalonamento de ônibus planejamento de tráfego eficiência do sistema

Luz Misteriosa em Mausoléu de Bruxelas: Coincidência ou Design?

2025-06-11
Luz Misteriosa em Mausoléu de Bruxelas: Coincidência ou Design?

A cada 21 de junho, ao meio-dia, um raio de luz atravessa o teto de um mausoléu no Cemitério de Laeken, em Bruxelas, criando um coração de luz. Não está claro se isso foi intencional. Os ocupantes do túmulo morreram em 1916 e 1919, e o mausoléu foi construído em 1920. O designer é pouco conhecido, e os planos não mencionam a luz. O artigo também apresenta um poema inscrito no monumento de Sir Lawrence Tanfield (falecido em 1625), expressando o amor e a dor de sua esposa.

Leia mais
(www.futilitycloset.com)
Diversos mistério histórico design de mausoléu fenômeno de luz

Rios Tipográficos: Um Caso Curioso de Alinhamento Acidental

2025-05-19
Rios Tipográficos: Um Caso Curioso de Alinhamento Acidental

Você já notou como às vezes os espaços entre palavras em um texto impresso se alinham coincidentemente para formar 'rios' verticais de espaço em branco? Esse fenômeno, mais comum em fontes monoespaçadas com justificação total, geralmente é evitado por tipógrafos devido à sua natureza distraidora. O artigo cita um exemplo clássico de 12 linhas descoberto em 1988 e uma coleção de 1986, destacando a aleatoriedade intrigante dessa peculiaridade tipográfica.

Leia mais
(www.futilitycloset.com)
Design

Prova Visual: a² – b² = (a + b)(a – b)

2024-12-15
Prova Visual: a² – b² = (a + b)(a – b)

O blog Futility Closet apresenta uma prova visual da fórmula matemática a² – b² = (a + b)(a – b), citando a perspicaz observação de Sophie Germain: “Diz-se que a álgebra não passa de geometria escrita e a geometria não passa de álgebra diagramática.” A publicação utiliza um diagrama de fácil compreensão para demonstrar a fórmula, destacando a elegância da matemática e a forte relação entre álgebra e geometria.

Leia mais
(www.futilitycloset.com)
Diversos prova matemática geometria álgebra