公交车调度难题:为何加车反而无效?
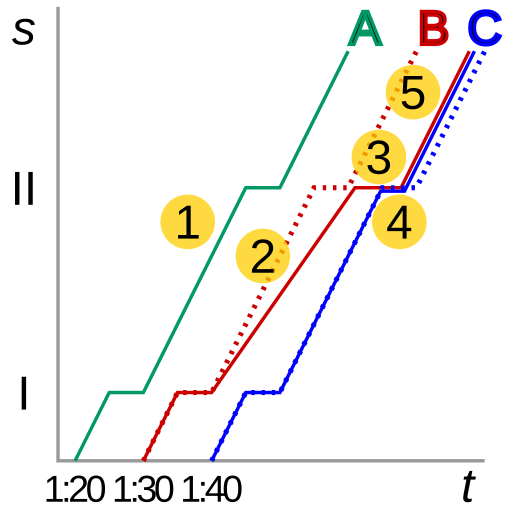
想象一下:两辆公交车按计划运行同一线路,但一辆因堵车延误。延误的公交车会捡到原本打算乘坐下一班车乘客,导致进一步延误。而下一班车则因乘客减少而提速。最终,两辆车会形成车队,甚至后车超过前车。增加车辆并非解决方法,更有效的方法是控制停站时间、跳站、引导乘客选择后车,甚至像北亚利桑那大学那样,放弃固定的时刻表,通过人为控制车距来保持均衡。
阅读更多
想象一下:两辆公交车按计划运行同一线路,但一辆因堵车延误。延误的公交车会捡到原本打算乘坐下一班车乘客,导致进一步延误。而下一班车则因乘客减少而提速。最终,两辆车会形成车队,甚至后车超过前车。增加车辆并非解决方法,更有效的方法是控制停站时间、跳站、引导乘客选择后车,甚至像北亚利桑那大学那样,放弃固定的时刻表,通过人为控制车距来保持均衡。
阅读更多
每年6月21日中午,一束光线穿透布鲁塞尔拉肯墓地一座陵墓的屋顶,形成一个光之心脏。这是否是刻意设计?陵墓的主人Louise Flignot和Léonce Evrard分别于1916年和1919年去世,陵墓直到1920年才建成。设计师Georges deLarabrie鲜为人知,设计图纸中也没有提到这个光之心脏。文章还提及了1625年去世的Sir Lawrence Tanfield墓碑上的诗歌,诗歌表达了妻子对丈夫的爱和思念。
阅读更多
你有没有注意到,有时印刷文本中单词间的空格会巧合地排列成一条条垂直的“河流”?这种现象通常发生在等宽字体和完全对齐的排版中,因为它会分散注意力,所以排版师通常会避免它。文章中提到了一个1988年发现的经典案例,以及一个1986年收集的“河流”效应的例子,这些例子说明了这种排版现象的趣味性和偶然性。
阅读更多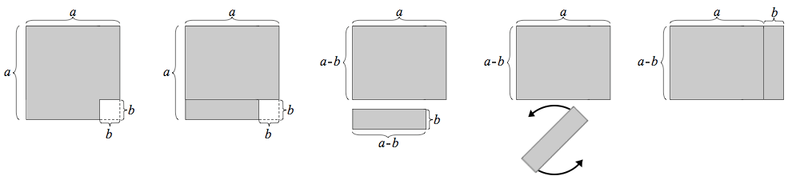
Futility Closet网站发布了一篇关于数学公式a² – b² = (a + b)(a – b)的视觉证明文章。文章引用了数学家索菲·热尔曼的名言:“据说代数只是书写的几何,几何只是图解的代数。” 这篇文章通过直观的图形展示了该公式的证明过程,体现了数学的简洁之美,也佐证了代数与几何的紧密联系。
阅读更多
爱因斯坦和哥德尔是亲密的朋友,他们每天都会在普林斯顿高等研究院之间往返步行。爱因斯坦很珍惜与哥德尔在一起的时光,他们的对话涵盖政治、哲学和物理等多个领域。与爱因斯坦的超高人气不同,哥德尔并不为名声所扰。
阅读更多
这篇文章介绍了Borwein积分,这是一系列由数学家David和Jonathan Borwein在2001年提出的数学公式。这些积分看似简单,但当引入sinc(x/15)因子时,结果会出乎意料地发生变化。文章引用了Hanspeter Schmid的解释,他认为这种现象并非软件错误,并提供了图形解释。
阅读更多
该网站是“无用小知识宝库”系列文章的一部分,专门探讨历史上有趣但不一定有用的事实。这篇文章讨论了1967年由美国陆军制定的“第3号协议”,该协议规定在紧急情况下使用化学和生物武器。作者认为,尽管存在争议,但该协议在冷战期间防止了核战争,并详细介绍了该协议的制定过程和后果。
阅读更多