Nichtlineare Verallgemeinerung der Maxwell-Gleichungen aus einem Variationsansatz
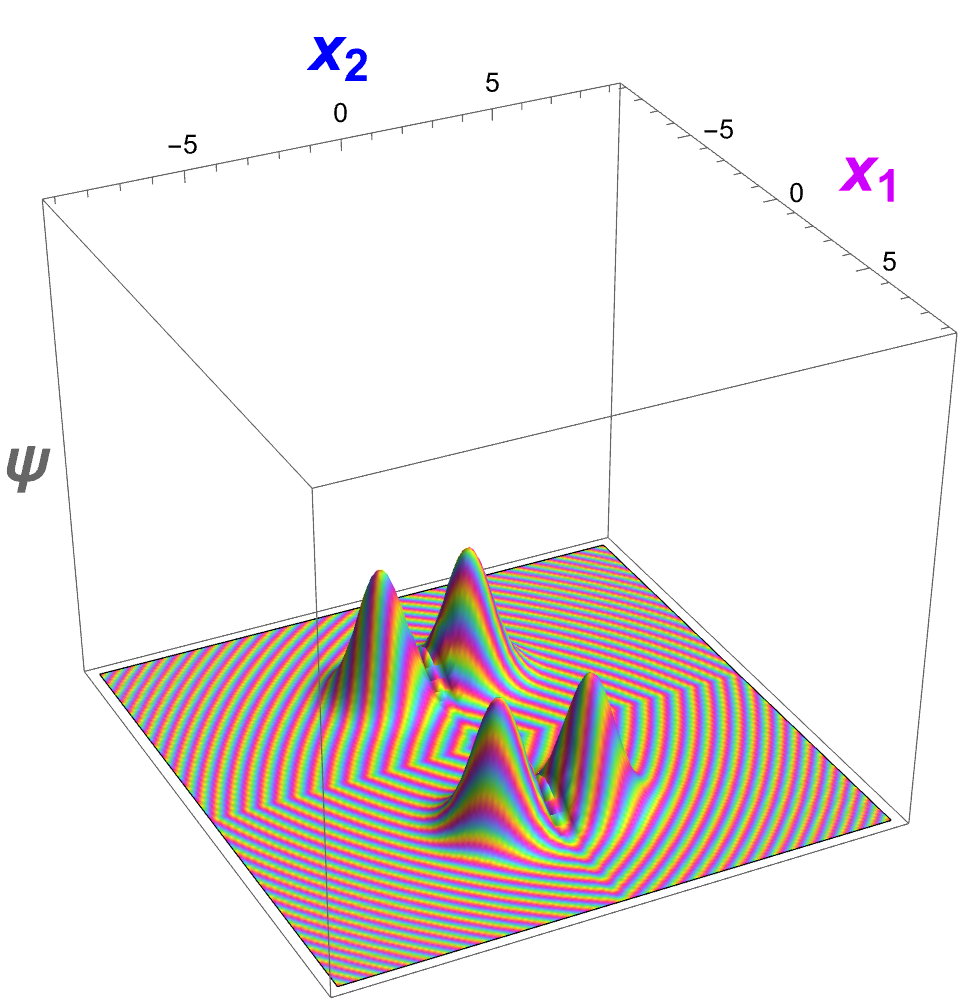
Dieser Forschungsartikel leitet eine nichtlineare Verallgemeinerung der Maxwell-Gleichungen aus einem Variationsansatz ab, wobei die Wirkung die Variabilität des metrischen Tensors misst. Der Raum ist ein Weyl-Raum, in dem die kovariante Ableitung des metrischen Tensors nicht verschwinden muss. Das Lorentz-Kraftgesetz wird als geodätische Gleichung hergeleitet. Die Ladungsdichte gehorcht einer kovarianten Wellengleichung, was darauf hindeutet, dass es sich um ein Feld handelt, das sich mit Lichtgeschwindigkeit ausbreitet, was die Wellennatur von Elektronen unterstützt. Die Dirac-Gleichung wird ebenfalls als geometrisch gezeigt. Der Zusammenhang zwischen der Lorentz-Kraft und der Raumzeitmetrik erklärt direkt den Zitterbewegung und die quantenmechanischen Wellen.