美国政府通过与Meta、谷歌、苹果等科技巨头合作，获得了对公民日常生活的惊人监控能力。近十年来，这三家公司向政府提供了超过300万个账户的详细信息，数据请求量激增。政府利用这些数据进行调查，但同时也引发了隐私担忧，因为这些请求中许多缺乏司法审查，甚至可能导致冤假错案。科技公司为维护自身商业模式，难以有效保护用户隐私，最终成为政府监控的帮凶。
阅读更多
Konga Beat是一款为任天堂GameCube游戏《大金刚咚咚咔2&3》设计的自定义曲目编辑器。它允许用户基于WAV或MP3音频文件创建新的曲目，并以游戏可读取的格式（.MID和.DSP）导出，以便在模拟器或GameCube主机上游玩。该编辑器支持多种难度（猴子、黑猩猩、大猩猩）和模式（标准、对战和挑战），并拥有易于使用的界面。
阅读更多
美国无人机产业发展受阻，其原因并非技术落后，而是FAA过时的法规限制了商业化无人机的大规模应用。与之形成对比的是，欧洲相对宽松的监管环境催生了像Manna这样的无人机公司，其商业成功为军事应用奠定了基础。文章指出，发展蓬勃的商业无人机市场能够重振美国国防工业的竞争力，降低成本，加速创新，摆脱对现有国防承包商的依赖，如同二战时期洛克希德公司因民用飞机生产而受益一样。作者呼吁美国学习欧洲和中国的经验，简化法规，支持商业无人机发展，才能在未来国防竞争中占据优势。
阅读更多
1929年，在伊斯坦布尔的托普卡帕宫，一位德国神学家偶然发现了一张由14世纪奥斯曼海军上将皮里·雷斯绘制的羊皮纸地图。这张地图以惊人的精度描绘了南美洲和非洲的海岸线，甚至包括南极洲的部分轮廓，这在当时的技术条件下是不可思议的。它整合了至少20张地图的资料，其中可能包括哥伦布的地图。皮里·雷斯地图并非简单的艺术创作，而是采用了先进的航海制图技术，例如使用罗盘玫瑰和航线，其精度让现代科学家也感到困惑。它不仅展现了当时航海技术的巅峰，更体现了不同文化交流与人类智慧的结晶。
阅读更多
NASA的Artemis III任务计划将三种植物——芥菜、一种芸苔和一种浮萍——送上月球表面。这些植物将被放置在一个特殊的生长室中，暴露在月球重力和辐射下，以研究月球环境对植物生长的影响。该实验旨在探索“生物再生”生命支持系统的可行性，为未来长期太空任务中宇航员提供空气、食物和水。实验结束后，部分植物将带回地球研究，剩余部分留在月球上继续监测，直到它们在月球夜晚冻死。该项目还将测试在月球上种植植物的技术挑战，例如如何应对强辐射和低重力环境。
阅读更多
西方世界面临诸多挑战：经济增长放缓、气候变化、健康问题、金融不稳定等等。但文章指出，这些问题的根源可能在于一个被忽视的因素——住房短缺。高昂的房价不仅导致人们生活成本增加，更重要的是，它影响了人们的居住地、工作、家庭规模甚至健康状况。住房短缺限制了生产力增长，扼杀了创新，加剧了不平等，并导致地区发展失衡。文章呼吁解决住房短缺问题，这不仅能降低房价，还能提高整体生活水平，促进社会和谐发展。
阅读更多/cdn.vox-cdn.com/uploads/chorus_asset/file/25639989/gmailbimi.png)
Gmail 的蓝色验证标记将出现在 iOS 和安卓移动应用程序上，适用于已采用谷歌品牌标识识别功能 (BIMI) 的发件人。这些标记之前仅在 Gmail 网页版客户端可见。谷歌现在还支持通用标记证书 (CMC)，这将允许“更广泛的发件人使用 BIMI”。
阅读更多
开发者Jeff Johnson发现Xcode在构建项目时频繁连接Apple服务器，导致构建速度变慢，尤其是在“收集供应输入”阶段。他通过Little Snitch禁用与developerservices2.apple.com的连接后，解决了构建速度问题。此外，他还发现Xcode在启动和打开项目时也会连接到其他Apple服务器，例如devimages-cdn.apple.com和appstoreconnect.apple.com，这些连接似乎并非必需，并可能上传开发者信息给Apple。Jeff认为Xcode的行为如同一个开发者数据收集工具，侵犯了开发者隐私。
阅读更多
文章探讨了异步 IO 的优缺点，并将其与多线程进行了比较。作者认为，尽管异步 IO 在处理高并发场景中具有优势，但其复杂性也增加了开发难度。作者提出，如果将过去几十年投入异步 IO 的资源用于改进操作系统线程的效率，或许能提供更简单、高效的解决方案。然而，由于现有操作系统的线程成本较高，异步 IO 仍然是目前处理高并发场景的必要选择。
阅读更多
Buzzinga.io 是全球最佳的 Jeopardy 游戏创建工具，允许用户创建和主持自定义 Jeopardy 游戏。该平台非常适合游戏之夜、课堂活动、企业培训和社交活动，无需注册即可使用。它提供内置蜂鸣器支持、自动分数统计、轻松的主持人控制以及高度可定制的类别和线索，包括文本、音频、图像和视频。
阅读更多
1980年圣海伦斯火山爆发后，科学家进行了一项实验，将囊鼠放入被火山灰覆盖的区域。结果发现，囊鼠的挖掘活动将含有益细菌和真菌的旧土壤带到地表，促进了植物的再生。实验后六年，囊鼠活动区域的植物数量显著增加，而未经处理的区域仍然贫瘠。这项研究表明，即使是像囊鼠这样不起眼的生物，也能在生态系统恢复中发挥重要作用，特别是土壤中的微生物和真菌对植物再生至关重要。
阅读更多
麻省理工学院开设了一门关于生成式AI的公开课，重点讲解基于流程匹配和扩散模型的数学框架。课程从第一性原理出发，涵盖了普通和随机微分方程、条件和边际概率路径等核心概念，并通过三个实验让学生动手构建一个简单的图像扩散模型。课程面向希望深入理解生成式AI理论和实践的学生，需要一定的线性代数、实分析和概率论基础，以及Python和PyTorch经验。
阅读更多
学习阿拉伯语的难点在于其复杂的字母和句子结构。本网站“Learn Arabic”另辟蹊径，无需先学习字母表，即可直接开始阅读阿拉伯语单词和句子。网站包含8261个阿拉伯语单词和2625个句子短语，每个单词和句子都带有详细解释和链接，方便学习者理解其含义和构成。此外，网站还利用阿拉伯语词根系统和单词模式的关联性，帮助学习者更好地记忆和理解新单词。这种独特的学习方法，让学习阿拉伯语变得更加轻松有趣。
阅读更多
openpilot是一个开源的机器人操作系统，目前支持超过275种车型的驾驶辅助系统升级。它由comma.ai开发，并接受社区贡献。openpilot需要配合comma 3/3X设备和相应的车辆线束使用，并提供驾驶数据收集功能以改进模型。需要注意的是，openpilot目前处于alpha测试阶段，仅用于研究目的，用户需自行承担使用风险。
阅读更多
为了应对美国严重的住房短缺和高昂的房价，马里兰州蒙哥马利郡正在建设一种新型的混合收入公寓，为不同收入水平的人提供住房。该项目由政府出资，部分公寓以市场价格出租，为低收入人群的廉租房提供资金支持。这种模式被称为“社会住房”，其优势在于能够永久性地提供保障性住房，并且不受私人投资者市场波动的影响。
阅读更多
这篇文章详细分析了 Griffin iMate ADB 转 USB 适配器中一个未公开电池的作用。作者修复了一个存在 USB 连接问题的旧 iMate，发现问题是由电池耗尽导致的电路噪声引起的。作者详细解释了 iMate 的电路设计，特别是它如何与苹果早期 USB 键盘中一个特殊电源按钮功能交互。
阅读更多
《阿凡达：最后的空气骑士》的原班人马将打造一部全新的26集2D动画剧集《阿凡达：七港》。故事设定在一个被灾难摧毁的世界，一位年轻的土元素掌控者发现自己成为了新的阿凡达，但她却面临着来自人类和灵界的敌人追捕。她和失散已久的双胞胎必须揭开神秘的身世，拯救文明最后的据点——七港。这部剧集由尼克儿童频道和阿凡达工作室制作，标志着阿凡达宇宙的持续扩展。
阅读更多
世界顶级棋手卡尔森将因“牛仔裤事件”而闻名的意大利Corneliani牛仔裤进行拍卖，所得款项将捐赠给美国大哥哥大姐姐组织。此前，卡尔森在世界快棋和闪电棋锦标赛上因穿着牛仔裤违反着装规定而被罚款并退赛，引发了“牛仔门”事件。这件32码的牛仔裤目前在eBay上的竞价已达8200美元，拍卖将于3月1日结束。此次慈善拍卖将用于支持该组织的青少年辅导项目，通过象棋诊所和社区活动帮助更多年轻人。
阅读更多
Mozilla计划在所有平台上禁用HTTP/2推送功能。原因是使用率低，并且存在一些仅影响 Firefox 的兼容性问题。其他浏览器，如 Chrome 和 Safari，已经禁用或不支持此功能。Mozilla建议使用 rel="preload" 和 103 Early Hints 作为替代方案。
阅读更多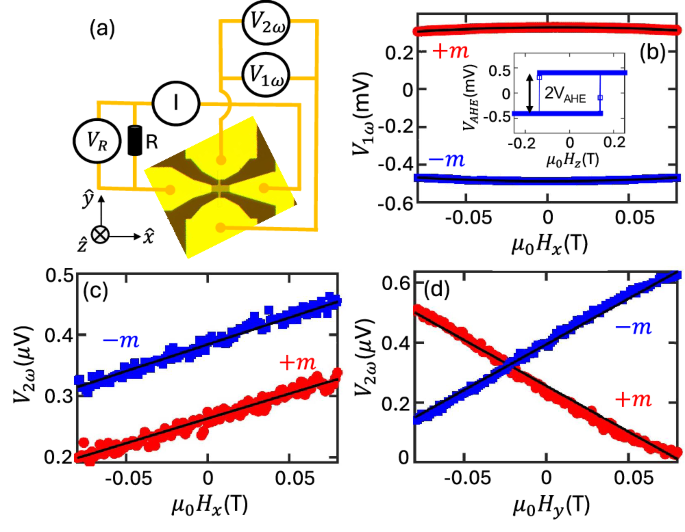
研究人员通过在垂直磁化[Co/Ni]3铁磁层中结合Ru、Nb和Cr等材料的轨道霍尔效应(OHE)，显著提高了自旋轨道矩(SOT)磁随机存取存储器(MRAM)器件的性能。实验结果表明，Ru/Pt OHE层相比纯Pt层，阻尼型扭矩效率提高了约30%，致使超过250个器件的开关电流降低了约20%，开关功率降低了超过60%。这项研究为高密度缓存存储器应用中的下一代SOT-MRAM器件性能提升提供了新的途径。
阅读更多
Mineflow 是一家致力于矿产勘探的人工智能平台，该公司正在招聘一名创始机器学习工程师。应聘者需要设计和实现模型架构和训练方案，以最大限度地提高海量地质数据集的性能，并与 Mineflow 团队紧密合作，进一步提高模型训练/推理的准确性和延迟。
阅读更多
1Password 推出了一个基于位置的新功能，允许用户为密码条目添加物理位置标签。当用户靠近某个凭证的位置时，该信息会显示在 1Password 移动应用程序中。此“附近项目”功能使 1Password 用户能够快速访问最相关的信息，无需搜索正确的详细信息或准确记住帐户的名称。位置信息可以添加到 1Password 账户中的任何新项目或现有项目。该应用程序还更新了地图视图，用于设置和查看项目的地理位置。1Password表示，用户的位置坐标仅在本地使用，不会离开设备。
阅读更多
美国纽约Qunnect公司的科学家们在纽约市地下进行了一项量子互联网原型网络测试。他们使用了一种名为GothamQ回路的34公里长光纤电路，利用偏振纠缠光子实现了长达15天的连续运行，系统正常运行时间高达99.84%。这项研究解决了光纤环境中纠缠态的脆弱性和信号传输效率问题，为量子互联网的实际应用迈出了重要一步。
阅读更多
萤火虫航天公司计划于美国东部时间3月2日凌晨3:34之前，利用搭载NASA科技的“蓝色幽灵”月球着陆器尝试月球着陆。“蓝色幽灵”预计降落在月球正面东北象限的危海附近，这是NASA商业月球有效载荷服务（CLPS）计划和阿尔忒弥斯计划的一部分，旨在建立长期月球存在。“蓝色幽灵”着陆直播将于美国东部时间凌晨2:20在NASA+播出，大约提前75分钟。
阅读更多
Assembled公司通过使用大型语言模型(LLM)编写测试，极大地提高了工程效率。LLM可以快速生成全面的测试套件，将原本需要数小时的任务缩短至几分钟。文章详细介绍了如何构建有效的LLM提示，以生成不同编程语言和测试场景的测试代码，并提供了一些实际应用案例。文章还强调了使用LLM进行测试时需要注意的事项，例如迭代优化、测试逻辑检查、提示定制和代码可测试性等。
阅读更多
这篇文章列出了《像计算机科学家一样思考：交互版》这本书的目录，涵盖了 Python 编程的基础知识，包括数据类型、控制流、函数、数据结构、面向对象编程等。还包括调试、模块、递归、GUI 编程、文件处理等高级主题。
阅读更多
作者呼吁大家建设属于自己的个人网站，对抗如今商业化、中心化的网络环境。文章追溯了早期网络的个人化魅力，对比了如今千篇一律的商业网站和依赖大型平台带来的数据隐私风险。作者鼓励读者以个人兴趣为出发点，创建独特的在线空间，表达自我，掌控内容，并推荐了一些便捷的建站工具和平台，例如Neocities。这篇文章体现了对网络去中心化理想的回归，以及对独立创作精神的呼唤。
阅读更多
